これまでご紹介してきた全波整流回路ですが、455kHz程度までなら実用可能なレベルと思います。さらに高周波までの正確な整流を期待する場合には、理想ダイオードの回路を根本的に考え直さなければなりません。
図1は、二つのNPNトランジスタのエミッタ・フォロワ出力を接続した回路です。次に、この回路の動作を考えてみることにしましょう。
![]() 高速動作対応の全波整流回路の設計
高速動作対応の全波整流回路の設計
これまでご紹介してきた全波整流回路ですが、455kHz程度までなら実用可能なレベルと思います。さらに高周波までの正確な整流を期待する場合には、理想ダイオードの回路を根本的に考え直さなければなりません。
図1は、二つのNPNトランジスタのエミッタ・フォロワ出力を接続した回路です。次に、この回路の動作を考えてみることにしましょう。
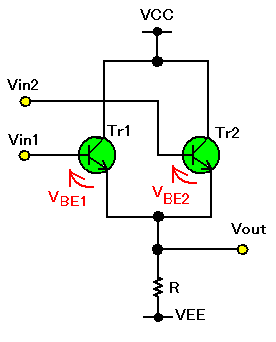 |
| 図1.二つのエミッタ・フォロワの出力接続回路 |
二つのNPNトランジスタのエミッタ・フォロワ出力を接続すると、図2(a),(b)に示すように入力端子Vin1とVin2で、端子電圧の大きい方が出力に得られます。すなわち絶対値回路になるわけです。
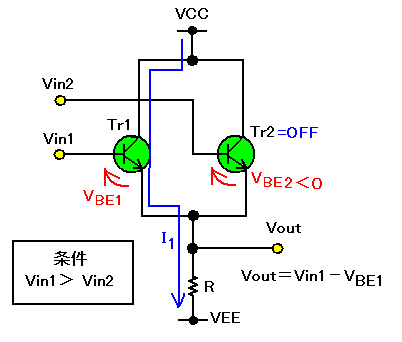 |
| 図2(a). 入力電圧が、Vin1>Vin2 のときの動作 |
図2(a)は、二つのNPNトランジスタのエミッタ・フォロワ出力接続回路で、入力電圧がVin1>Vin2の条件での動作を示します。このとき、入力電圧が大きい方のトランジスタTr1が動作し、Tr2はOFFします。したがって、トランジスタを流れる電流は図2(a)のように、Tr1の方へ流れます。
さて、出力電圧ですが、トランジスタTr1のベース・エミッタ間の電位差はVBE1となるので、Vout=Vin1−VBE1 となります。VBE1の値は、シリコントランジスタであれば概ね0.7V程度になります。したがって、出力電圧は入力電圧よりも0.7V低くなります。
一方、Tr2のVBE2ですが、逆方向にバイアスされるため、VBE2<0になっています。
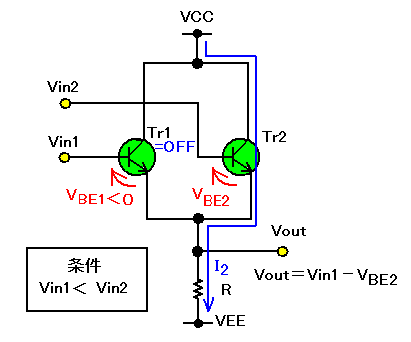 |
| 図2(b). 入力電圧が、Vin1<Vin2 のときの動作 |
図2(b)は、二つのNPNトランジスタのエミッタ・フォロワ出力接続回路で、入力電圧がVin1<Vin2の条件での動作を示します。このとき、入力電圧が大きい方のトランジスタTr2が動作し、Tr1はOFFします。したがって、トランジスタを流れる電流は図2(b)のように、Tr2の方へ流れます。出力電圧は、Vout=Vin2−VBE2 となります。
ですから、一方のエミッタ・フォロワにVinを入力し、他方に−Vinを入力すれば、Vinの絶対値が得られることになります。
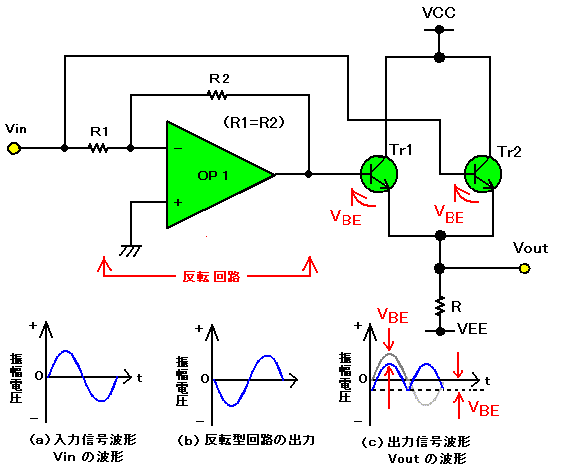 |
| 図3. 二つのエミッタ・フォロワの出力接続回路を用いた全波整流回路 |
図3は、二つのエミッタ・フォロワの出力接続回路を用いた全波整流回路を示します。トランジスタTr2の入力にはVinをそのまま接続しますが、トランジスタTr1の入力には反転回路を接続します。したがって、図3(a)の入力信号VinはTr2の入力信号波形に相当し、図3(b)の反転回路の出力波形はTr1の入力信号波形に相当します。図3(c)に、この全波整流回路の出力信号波形Voutを示します。
これまで述べてきたように、この回路では出力にエミッタ・フォロワをそのまま用いているので、VBE分だけ電圧が下がります。約0.7Vも!! これはかなり大きい誤差です。しかし、図4のように少し出力回路を変えるノウハウで、誤差を減らすことができます。
 |
| 図4.エミッタ・フォロワの出力補正回路 |
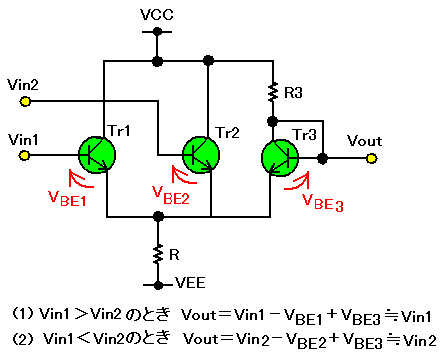
図4に、エミッタ・フォロワ回路のVBE低下誤差を補正する回路ノウハウを示します。
これは、Tr1あるいはTr2により、VBEだけ下がった電位を、Tr3を用いて持ち上げてやろうというものです。
すなわち、Vin1>Vin2のとき、Vout=Vin1−VBE1+VBE3ですが、VBE1=VBE3となるようにすれば、Vout≒Vin1とすることが可能です。同様にして、Vin1<Vin2のとき、Vout=Vin2−VBE2+VBE3で、VBE2=VBE3となるようにすれば、Vout≒Vin2となります。Tr1,Tr2,Tr3を特性のそろったトランジスタを使うことも大事ですが、VBEの値をそろえるようにR3の抵抗値を最適にして、Tr3を流れる電流値と、Tr1もしくはTr2がONのときの電流値を、概ね同じにする必要があります。
その他の注意点としては、トランジスタがOFFとなるときのベース・エミッタ間電圧が、Vin1とVin2との差分だけ逆バイアスされます。一般に、ベース・エミッタ間の耐圧はあまり高くないので(2SC1815は、約5V)、信号振幅はそれ以下に抑える必要があります。
![]() 少ない高精度抵抗で作る全波整流回路の設計
少ない高精度抵抗で作る全波整流回路の設計
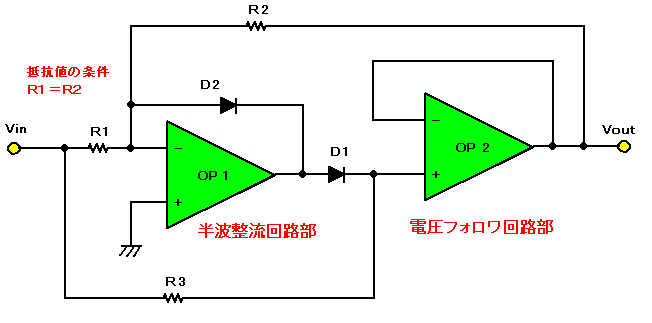
全波整流回路を精度良く作ろうと思うと、高精度抵抗が多数必要です。図5の回路では2本の高精度抵抗だけですみます。
 |
| 図5. 少ない高精度抵抗で作る全波整流回路 |
この回路は、理想ダイオード回路OP1と、電圧フォロワOP2を組み合わせたものと考えられます。この回路の動作を考えてみましょう。
図6(a),(b)のように、入力電圧の正負で場合分けしてみると考えやすいです。
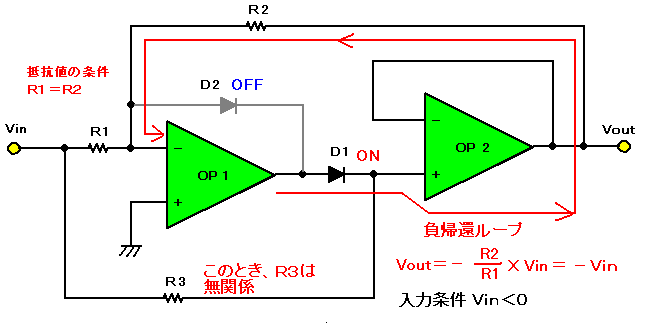 |
| 図6(a). 少ない高精度抵抗で作る全波整流回路の動作(入力電圧がVin<0のとき) |
入力電圧がVin<0のとき、ダイオードD2はOFFになり、D1が導通します。このとき図に示すように、D1,OP2,R2を通る負帰還ループができます。入力端子と半波整流回路部間にR3がありますが、出力電圧には何ら関係ありません。また、電圧フォロワのOP2ですが、帰還ループに入っていますので、これも出力電圧には何ら関係ありません。そうすると、R1,R2,OP1で構成される一般的な反転回路と同様に考えることができ、R1=R2であれば出力電圧はVout=−Vinとなります。
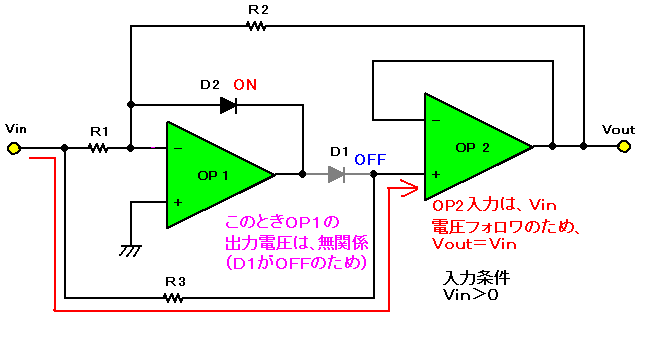 |
| 図6(b). 少ない高精度抵抗で作る全波整流回路の動作(入力電圧がVin>0のとき) |
入力電圧Vin>0のときは、D1がOFFになり、OP1の出力をOP2から切り離します。すなわち、OP1の出力電圧は何ら関係ありません。一方、OP2の入力はR3を通してVinが入力されます。OP2は電圧フォロワのため、出力はVout=Vinとなります。
抵抗値については、Vin<0のときにR1とR2の抵抗比だけが精度に影響し、R3は無関係です。ただし、D1の漏れ電流やOP2の入力バイアス電流がR3を流れることによって誤差を生じますから、極端に大きな値は避ける方が良いでしょう。また、精度は抵抗の絶対値ではなく抵抗比R1:R2に依存しますから、抵抗アレイを用いて精度を向上できます。また、トリマで調整する場合でも、R1の一箇所だけですみます。なお、当然のことながら、Vinの信号源抵抗はR1に比べて十分に小さい必要があり、無視できない場合それがそのまま誤差となります。このような場合は、入力にバッファ・アンプなどをつけるようにします。
![]() OPアンプ1個で作る全波整流回路の設計(その1)
OPアンプ1個で作る全波整流回路の設計(その1)
精度は多少悪くなりますが、図7に示すようにOPアンプ1個だけでできる全波整流回路を紹介します。抵抗の数も3本(精度に影響するのはそのうち2本)ですみます。
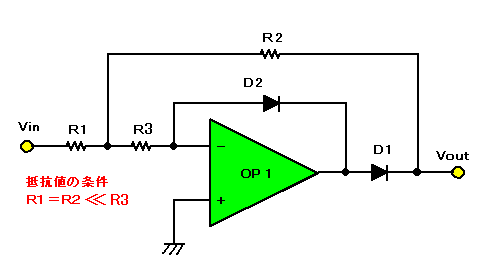 |
| 図7. OPアンプ1個で作る全波整流回路1 |
この回路は、反転型の理想ダイオードに抵抗R3を挿入したものと考えられます。この回路の動作を考えてみましょう。
図8(a),(b)のように、入力電圧の正負で場合分けしてみると考えやすいです。
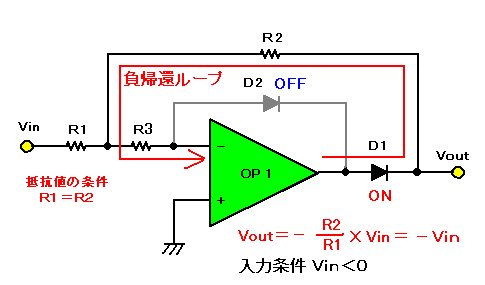 |
| 図8(a). OPアンプ1個で作る全波整流回路1の動作(入力電圧Vin<0のとき) |
Vin<0のときは、D1が導通してD1,R2,R3を通る負帰還ループができます。ここで、R3を流れる電流が無視できるくらい小さければ、R1とR2の分圧点の電圧は0となり、一般の反転型回路とみなせます。R1=R2であれば、出力Vout=−Vinが得られます。
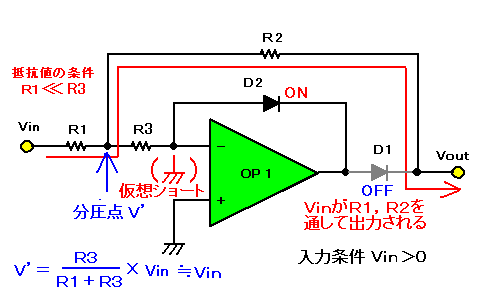 |
| 図8(b). OPアンプ1個で作る全波整流回路1の動作(入力電圧Vin>0のとき) |
入力電圧Vin>0のときは、D1がOFFになり、OP1の出力をVout端子から切り離します。すなわち、OP1の出力電圧は何ら関係ありません。OP1の反転入力端子は仮想ショートとなっているため、OP1側のR3は0Vとみなせます。したがって、このときR1とR3の分圧点V’から出力Voutを取り出すことになり、Vout={R3/(R1+R3)}×Vinとなります。
ここで、R3>>R1であれば、Vout=Vinとみなすことができます。このように、図7の回路は全波整流回路として働くわけですが、精度の面から若干の制約があります。といっても、1%程度の精度は無理なく実現できますから、精度を重視する回路でなければ十分に実用になります(^^;)。
精度向上のノウハウは、Vin>0のとき精度がほぼR3/(R1+R3)で決まりますから、R3とR1の抵抗比を十分大きくとることです。R1(=R2)については、抵抗値をあまり小さくとると、Vin<0のときにOPアンプの出力が過負荷になってしまいますから、一般には5kΩ〜10kΩぐらいが用いられます。一方、R3については、抵抗値をあまり大きくとると、ノイズを拾いやすくなりますし、また、Vin<0のときにR3での電圧降下が大きくなってしまいます。実用的には1MΩ程度が上限です。
また、Vin<0のときにR3を流れる電流を小さくするために、OPアンプにはFET入力のものを選びます。ダイオードD1にも、逆方向の漏れ電流が小さいものを選ぶ必要があります。また、この回路を用いる場合には、出力インピーダンスにも注意する必要があります。この回路は、Vin>0のとき出力インピーダンスが大きい(R1+R2で決まる)欠点があります。したがって、次段の回路の入力インピーダンスが小さい場合には、バッファが必要になり、部品点数が増えてしまいます。
![]() OPアンプ1個で作る全波整流回路の設計(その2)
OPアンプ1個で作る全波整流回路の設計(その2)
図9の回路は、OPアンプ1個、ダイオード2本,抵抗4本で全波整流回路を実現しています。
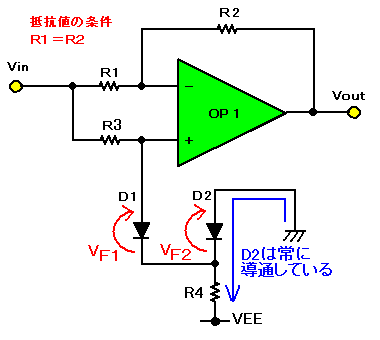 |
| 図9. OPアンプ1個で作る全波整流回路2 |
この回路の動作を考えてみましょう。図10(a),(b)のように、入力電圧の正負で場合分けしてみると考えやすいです。
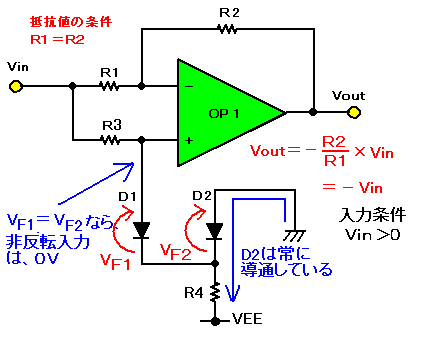 |
| 図10(a). OPアンプ1個で作る全波整流回路2の動作(入力電圧Vin>0のとき) |
ダイオードD2は常に導通してバイアス電圧(−VF2)を発生しています。このバイアス電圧は、ダイオードD1の順方向電圧VF1をうち消すためのものです。すなわち、D1がONのときにVF1=VF2であれば、OP1の非反転入力端子は0Vとみなせます。
入力電圧が正の半サイクル(Vin>0)では、D1が導通してOPアンプの非反転入力を0Vに保つので、回路はゲイン1の反転増幅回路となります。すなわち、Vout=Vinです。
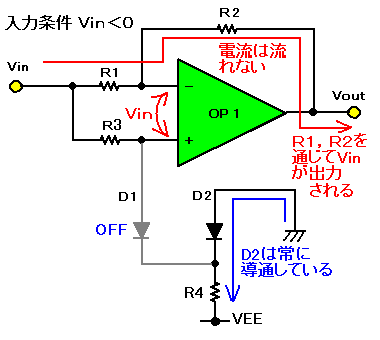 |
| 図10(b). OPアンプ1個で作る全波整流回路2の動作(入力電圧Vin<0のとき) |
入力電圧が負の半サイクル(Vin<0)では、D1は導通せず、OPアンプの非反転入力はR3を通して電圧Vinが加えられます。仮想ショートにより反転入力の電圧もVinであり、抵抗R1には電流が流れません。したがって、帰還抵抗R2にも電流は流れないことから、Vout=Vinとなります。すなわち、この回路はダイオードの順電圧の影響を受けずに全波整流を行うことができます。
OPアンプの仮想ショートが常に保たれて、OPアンプ自体の動作は不連続にならないので、反転と非反転の切り替え時に遅れを生じることなく、高速の動作が可能です。ただし、実際にはVF1とVF2に若干の差があるため、順電圧を完全にうち消すことはできず、精度が悪くなります。
全波整流回路については、その他にも様々な設計があると思います。部品点数がより少なく、精度よく、かつ高速(高い周波数)で使えるものが、設計の重要なポイントと思われます。皆さんも、時間があれば実際にブレッドボードなどで回路を組んで実験されてみることをお勧めします。
[次へ]は、検波回路総括のページへ。
 |
 |
 |
|